Random Beacons
The future of randomness will be unbiased, unpredictable, unobstructed, and publicly verifiable. How will this future be achieved? Via Cryptographic Beacons a.k.a Random Beacons.
Why should you want this future? Because it allows for trustworthy randomness in a distrustful world which facilitates both societal and economic gain. Random Beacon applications are wide varying, from enabling e-voting, general assemblies, fair audit of government officials and lotteries to more secure cryptographic schemes, quantum computing and efficient blockchain technologies.
In this post we will explore the principles of Random Beacons as well as three current State of the Art (“SOTA”) implementations; Hydrand, GRandPiper and BRandPiper.


But first, below is a live Random Beacon based on the DRand protocol which will emit values every 30 seconds to give you a practical idea of what these protocols output.
Live Random Beacon
Round Number:
Random Value:
Next Emission ETA: seconds
Note. Unsynchronised wall clocks may lead to inaccuracies in your ETA countdown.
Introduction to Random Beacons
A Random Beacon is responsible for the public emission of randomness. A variation of the concept was first published in 1983 by Rabin (who you may recognise from the famous Miller-Rabin primality test). Rabin proposed a “beacon” that would continuously emit randomly chosen integers at a specified time interval △. Recently there has been a lot more interest from academia due to its utility in proof-of-stake blockchain technology.
Let’s define a Beacon more formally:
- Definition 1: A continuous random beacon protocol produces randomised values at defined time intervals △. Where the emitted values display the properties of bias-resistance and unpredictability. Additionally, a desirable beacon protocol should demonstrate liveliness and public verifiability.
As you can see the core concept is quite simple. Let's define some of those aforementioned properties:
- Definition 1.a Bias resistance is demonstrated if an entity, malicious or otherwise, is unable to influence future emissions of the beacon.
- Definition 1.b Unpredictability is demonstrated if an entity, malicious or otherwise, is unable to predict future emissions of the beacon.
- Definition 1.c Liveliness is demonstrated if an entity, malicious or otherwise, is unable to prevent the progress of the protocol
- Definition 1.d Public verifiability is demonstrated if upon emission of a random value, any interested parties can verify the correctness of the emitted value using public information
From these definitions you can infer Random Beacon research is primarily interested in addressing the trustworthiness of random emissions as opposed to the quality of the entropy. If you’re interested in sources of entropy, check out the League of Entropy, a personal favourite is seismic measurements of earthquakes in Chile.
The Random Beacons we will explore are all decentralised protocols. This differs to a to a Random Beacon maintained by a single entity for example the V1 NIST Random Beacon, which to be used by a third party inherently requires trust in the integrity of the organisation. Remember requiring trust is something we want to avoid in the future of randomness.
Why are these properties necessary?
Let’s walk through an example application most have likely experienced, a “random” search at airport customs. With a random beacon travelers could be selected based on the current beacon emission. The emission would need to be bias resistant so that a bad actor couldn’t manipulate who was selected. Unpredictability and liveliness would be essential so that a bad actor couldn’t purposefully avoid a search. Finally, by supporting public verifiability the subject of the search could be sure their selection wasn’t a result of discrimination.
The motivating logic for other equity-based use cases such as lotteries and audits follows similarly.
What are the challenges in creating a Random Beacon?
The main challenges faced in Random Beacon research relate to the design of a protocol that can provide the properties outlined in Definition 1.a – 1.d whilst maintaining desirable communication complexity. A formal set of criteria to assess a protocol’s performance against these challenges was first provided by Schindler et al. in the HydRand paper and has since seen widespread academic adoption.
Understanding these challenges helps to better understand the technical contributions of Hydrand and the RandPiper suite, which we will discuss in later sections.
We will refer to Definition 1.a – 1.d as the “Fundamental Challenges” and introduce 5 additional challenges.
- C1: Communication complexity
- C2: Trusted setup / distributed key generation (“DKG”)
- C3: Fault tolerance
- C4: Adaptive adversary
- C5: Reusability
C1 refers to the total number of bits transferred between all nodes per emission of a random beacon value and is evaluated in standard Big O notation. Improving upon C1 results in a more scalable protocol and is considered a major focus, given beacon applications in blockchain systems (currently a major driver of research) will typically require scaling for large groups of nodes.
A desirable random beacon should not involve reliance on a trusted party as to avoid single points of failure. This challenge, C2, can be viewed as a binary classification and is motivated by the clear negation of a decentralized protocol’s total utility if the setup phase requires trusted parties.
An additional challenge C3, associated with Random Beacons is the ability to handle an increasing number of Byzantine nodes. The objective of C3 is to design for optimal Byzantine Fault Tolerance ("BFT") \( f = \frac{n}{2} \) over classical \( f = \frac{n}{3} \) where \( f \) throughout this post will represent dishonest nodes out of all \( n \) nodes. Satisfaction of C3 reduces the practical burden of assumptions on the number of honest nodes in the system.
C4, refers to the development for less restrictive assumptions on the occurrence of Byzantine Faults. Assuming an adaptive adversary such that both dishonest nodes can behave and faults occur, arbitrarily, is a much less restrictive assumption than a predetermined static alternative. Thereby satisfying this binary classification provides a more rigorously sound security bedrock for practical implementations.
The final challenge C5, is whether the protocol can continue to execute upon replacement of one of the participant nodes without requiring a re-execution of the set-up phase. This offers a practical benefit in efficiency and flexibility of the protocol.
SOTA Implementation: HydRand
HydRand is a synchronous random beacon designed to be a standalone implementation applicable to a variety of use cases and implementations. It’s major contribution is the provision of Guaranteed Output Delivery (“G.O.D”) and improved efficiency compared to similar beacon protocols based on Publicly Verifiable Secret Sharing (“PVSS”).
An execution of a HydRand round has three stages, namely Propose, Acknowledge and Vote. At the end of a round the Random Beacon value is computed, new leader selected uniformly based on the Beacon output and the next round begins. In the Propose stage (Figure 1), the leader 𝐿 is responsible for broadcasting a signed message to all other nodes. The signed message contains the leader’s previously revealed secret and encrypted shares for a new randomly picked secret.
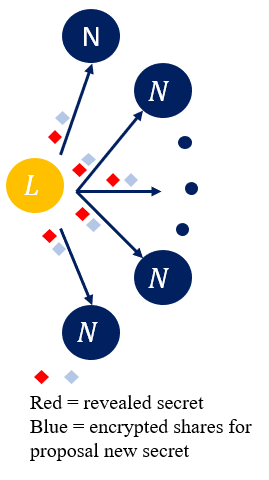
In the Acknowledge phase each node which previously received a valid message from the leader is required to broadcast a signed acknowledge message. This message includes the leader’s revealed secret and the hash and signature of the received proposal (Figure 2). This design ensures via the hash that any malicious node that attempts to subsequently distribute a different message in a future propose phase is detected. Furthermore, including the leader’s signature safeguards an honest leader from false accusation by a malicious node. These coupled, facilitate a mechanism for satisfying Definition 1.a.
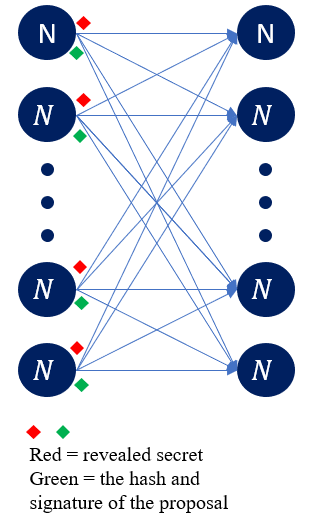
The vote stage then occurs (Figure 3). Nodes are required to broadcast either a signed confirm or recovery vote based on the acknowledge messages they received at conclusion of the previous stage. If a node has received 2𝑓 + 1 acknowledge messages for the leader’s proposal, then they will broadcast a confirm vote, otherwise a recover. A recovery message includes a decrypted version of the share of the previously proposed secret that node received. Which assists in enabling recovery of the leader’s shared secret if required upon conclusion of this stage and supports Definition 1.c-1.d.
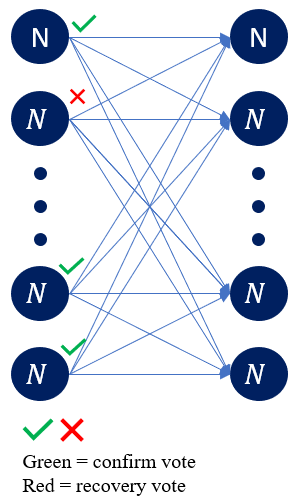
The Random beacon is then emitted depending on whether 2𝑓+ 1 confirm votes were transmitted or 𝑓 + 1 recovery votes. In the case of adequate confirm votes the secret 𝑆 can be directly identified. If 𝑓 + 1 recovery votes are received the decrypted shares of the leader’s previous proposal are used to reconstruct the secret hence facilitating G.O.D. This can be achieved due to the use of the underlying Scrape PVSS primitive (Cascudo & David, 2017) and because any node that did not fulfil their duties as a leader in a prior round are prohibited from re-election. The 𝑆 generated is equivalent regardless of identification method which supports satisfaction of Definitions 1.a,c. The hash of the secret is then combined with the previous Random Beacon emission to generate the Random Beacon output for the current round (Figure 4).
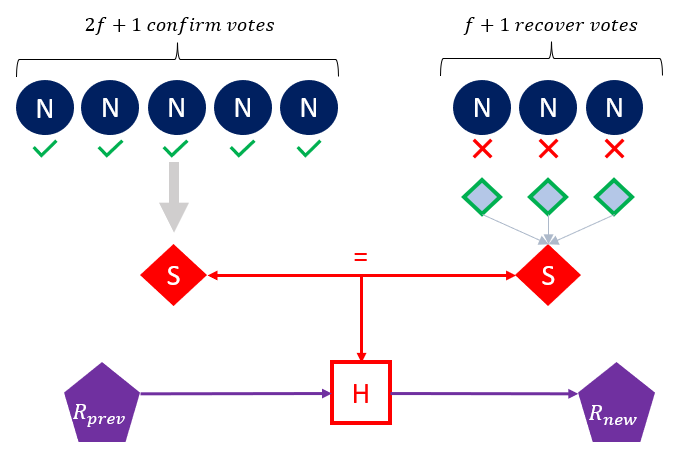
Compared to preceding schemes that also leverage PVSS, the HydRand protocol results in quadratic as opposed to cubic communication complexity. This O(n) improvement against C1 occurs because the 𝑛 sized communications are transmitted by only the leader node and messages to be broadcast by all nodes are constant complexity. The prior literature required linear sized broadcasts by all nodes to distribute PVSS shares.
The HydRand round design also results in no need for a trusted dealer or DKG in the initial setup phase, namely a public key exchange and initial commitment via PVSS are the only requirements. This is a significant contribution towards C2 which improves upon protocols such as RandHerd. That although offer logarithmic communication complexity do not satisfy C2.
SOTA Implementation: RandPiper Suite
RandPiper contributes two new Random Beacon Protocols, GRandPiper and BRandPiper, based on an underlying pipeline architecture (Figure 5). Furthermore, Bhat et al. contribute an improved Verifiable Secret Sharing (“iVSS”) protocol that is used in BRandPiper and improvements in conventional BFT SMR.
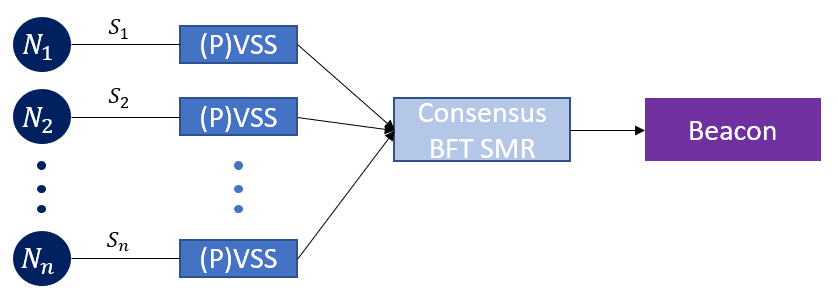
The improved BFT SMR protocol (Figure 6) underpinning RandPiper contributes to improvements against C3 whilst maintaining performance against C1 consistent with the best in class, assuming an honest leader and Byzantine nodes 𝑓 = 𝑂(1). Namely it achieves, \(𝑂(𝑘𝑛^2) \) communication complexity (C1) per epoch 𝑒, where k is a multiplicative constant security parameter, whilst achieving optimal fault resilience (C3) and no reliance on distributed key generation (partial C2). C2 is not fully satisfied because of the use of q-SDH assumptions in the setup phase, which to generate public parameters requires some variation of a trusted setup or secure computation protocol.
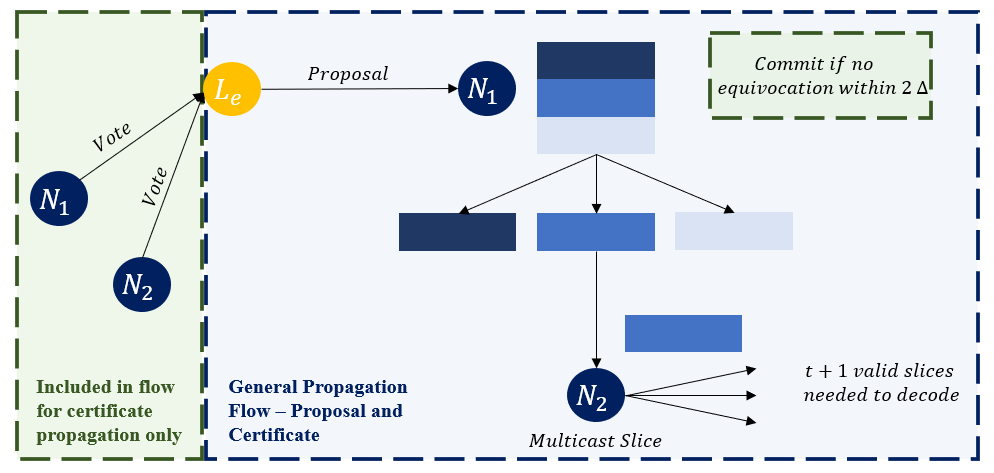
Figure 6 illustrates a simplified version of this protocol. The protocol’s objective is to ensure propagation of a linear size proposal hence avoiding the conventional cubic SMR complexity. The leader \( L_e \) broadcasts their proposal. If a node \( n_i \) (figure 6, 𝑖 = 1) receives the first rank extending certificate they then execute the deliver function which involves slicing this payload into 𝑛 slices, building off a linear erasure and error correcting code primitive, and generate the corresponding proofs / witness. This node then sends the slice to all other nodes. If a node \( n_j \) , (Figure 6, 𝑗 = 2) receives a valid slice for the accumulator primitive, note Bhat et al. demonstrate both a Merkle Tree and Bilinear variant, they then multicast this slice to all other nodes. Any node that has 𝑓 + 1 valid slices can then successfully decode. Crucially to avoid cubic communication complexity the nodes then send their votes only to the leader (shaded green block figure 6). The leader is then responsible for combining 𝑓 + 1 to create a single certificate, which therefore by definition ensures at least one must be truly random. This certificate then must be broadcast to all nodes, the same generic flow (blue shaded block in figure 6) can be used. Assuming no equivocation in 2 △ the proposed certificate can be committed
GRandPiper
Good Pipelined Random Beacon ("GRandPiper") is the first of the RandPiper protocols discussed. It contributes to C5 whilst achieving good C1 due to the underling BFT SMR, although C4 is not addressed with absolute unpredictability. In Figure 7 the architecture is depicted, note for each epoch 𝑒 a leader nominates a random value and a PVSS sharing to support secrecy and in turn Definition 1.a-b. This is then disseminated using the SMR protocol. A leader is not allowed to be re-elected until 𝑓 additional rounds have surpassed, which supports the unbiased property. Leaders are effectively required to commit their random values 𝑓 + 1 epochs in advance hence the values used to construct the beacon will be independent and recoverable regardless of the leader’s co-operation in the current round. In epoch 𝑒′ which represents the next time a leader is selected, their previously committed random value is recovered “PVSS R” and the beacon is generated as the Hash of that value and the previous beacon outputs. Should a leader not commit a random value they are prohibited from re-election. This ensures a future epoch is not impacted. Furthermore, as their previous commitment can be recovered without their input, the current epoch is robust. Thereby GRandPiper addresses Definition 1.c.
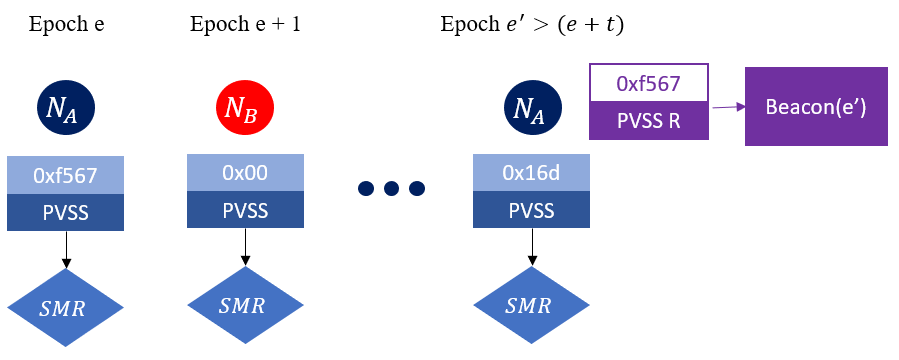
The primary contribution is in the form of optimal fault tolerance (C3) compared to prior literature based on PVSS such as Hydrand. However concurrent work such as RandRunner has also achieved optimal C3 but requires computationally expensive verifiable delay functions.
BRandPiper
Better Pipelined Random Beacon ("BRandPiper") is an extension of GRandPiper that is designed to provide optimal unpredictability without sacrificing communication complexity (C1) and supporting optimal fault tolerance (C3), adaptive adversaries (C4) and reconfiguration (C5).
Utilising PVSS to achieve absolute unpredictability typically results in cubic communicational complexity. Therefore, to avoid this RandPiper contributes iVSS which removes the need to “agree” on complaints. Conceptually, iVSS improves elements from efficient VSS such as the use of a bulletin board to reduce communication overhead. In iVSS, the dealer discreetly disseminates secret shares and witnesses whilst also posting commitments to the bulletin board. Nodes broadcast blame messages to all other nodes and forward these messages to the dealer to request the corresponding missing share. Rather than posting to the bulletin board the dealer responds to the blames privately. Assuming resolution of all their blame messages an honest node then sends an ACK to the dealer. Upon collating 𝑓 + 1 ACKs the dealer posts their ACK certificate to the bulletin and honest nodes can then commit.

In BRandPiper, Bhat et al. use their SMR protocol (C3) for establishing the bulletin board and block validation is an implementation of their proposed iVSS on a vector of VSS commitments. Practically, a round robin is conducted to select leaders and for each epoch the random shares \( 𝑟_{i,j} \) of all honest nodes are homomorphically combined to produce that round’s group random value \( R_j \) . This homomorphic combination of honest shares ensures the group value is random (Definition 1a-b) and assists in achieving absolute unpredictability. The hash of this group value is then emitted as the Random Beacon value for that epoch (Figure 8).
This results in best case quadratic communication complexity when the number of byzantine faults is constant, thereby cementing Bhat et al.'s contribution as an improved solution for providing secure optimal fault tolerance and unpredictability.
Comparing the Protocols
HydRand’s PVSS approach provides several non-trivial improvements including the removal of reliance on a trusted dealer and as shown in Figure 9 superior efficiency whilst still maintaining G.O.D. However, this is at the expense of optimal fault tolerance, a restrictive assumption prohibiting arbitrary occurrence of corruptions during the protocol execution and most importantly no absolute unpredictability. As such it’s practical utility for applications requiring utmost security is diminished.
BRandPiper benefits from its recency enabling it to address shortcomings in earlier literature. This is most apparent in a comparison to HydRand. As shown in below table, BRandPiper provides an optimal fault tolerance and unpredictability whist still achieving comparable communicational complexity. This comes from identifying opportunities for optimization in HydRand’s secret shares, namely its buffer characteristics and the failure to deliver PVSS shares to all honest nodes thereby not achieving optimal fault tolerance. As such BRandPiper is the most well rounded of the protocols discussed in this report. GRandPiper in comparison is largely superseded by BRandPiper and hence has limited stand-alone utility.
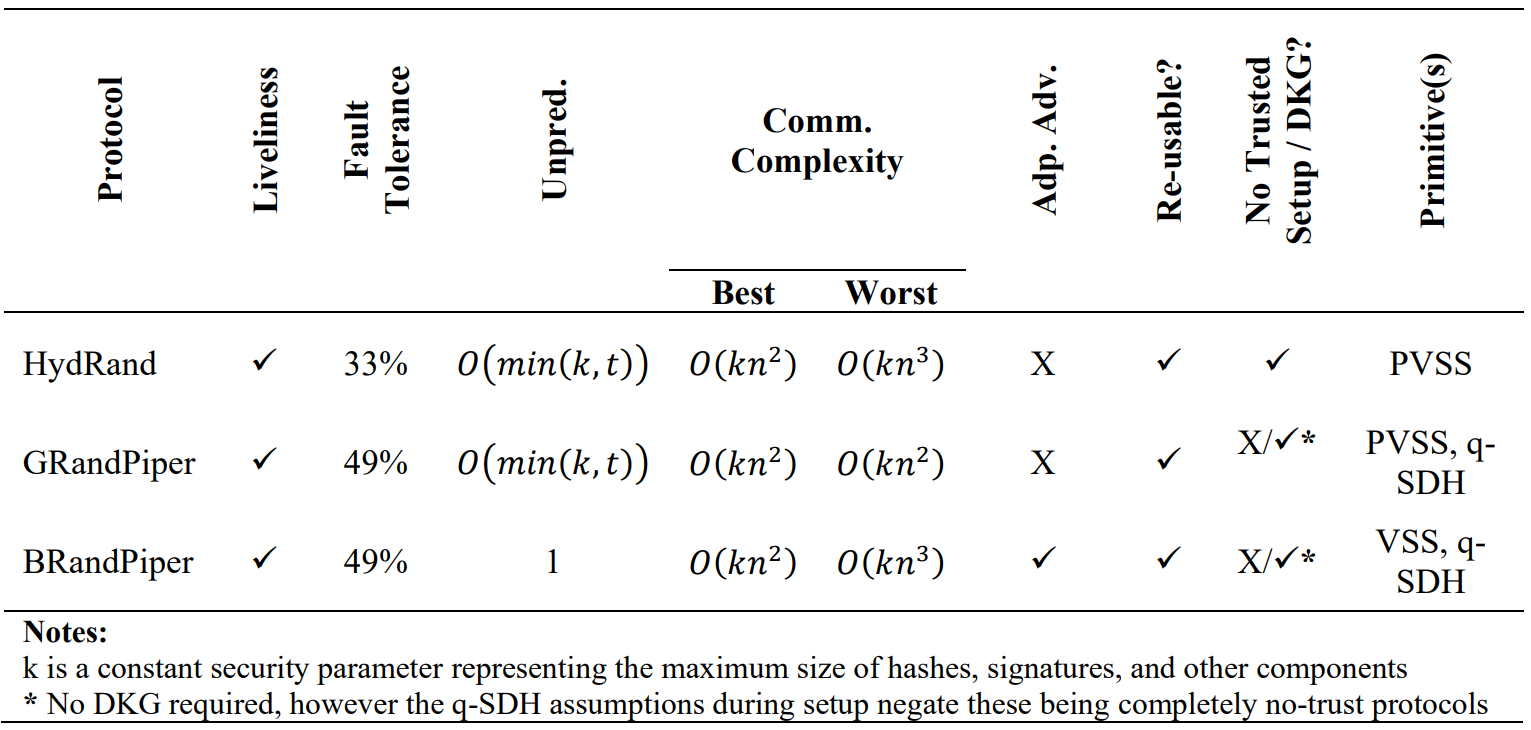
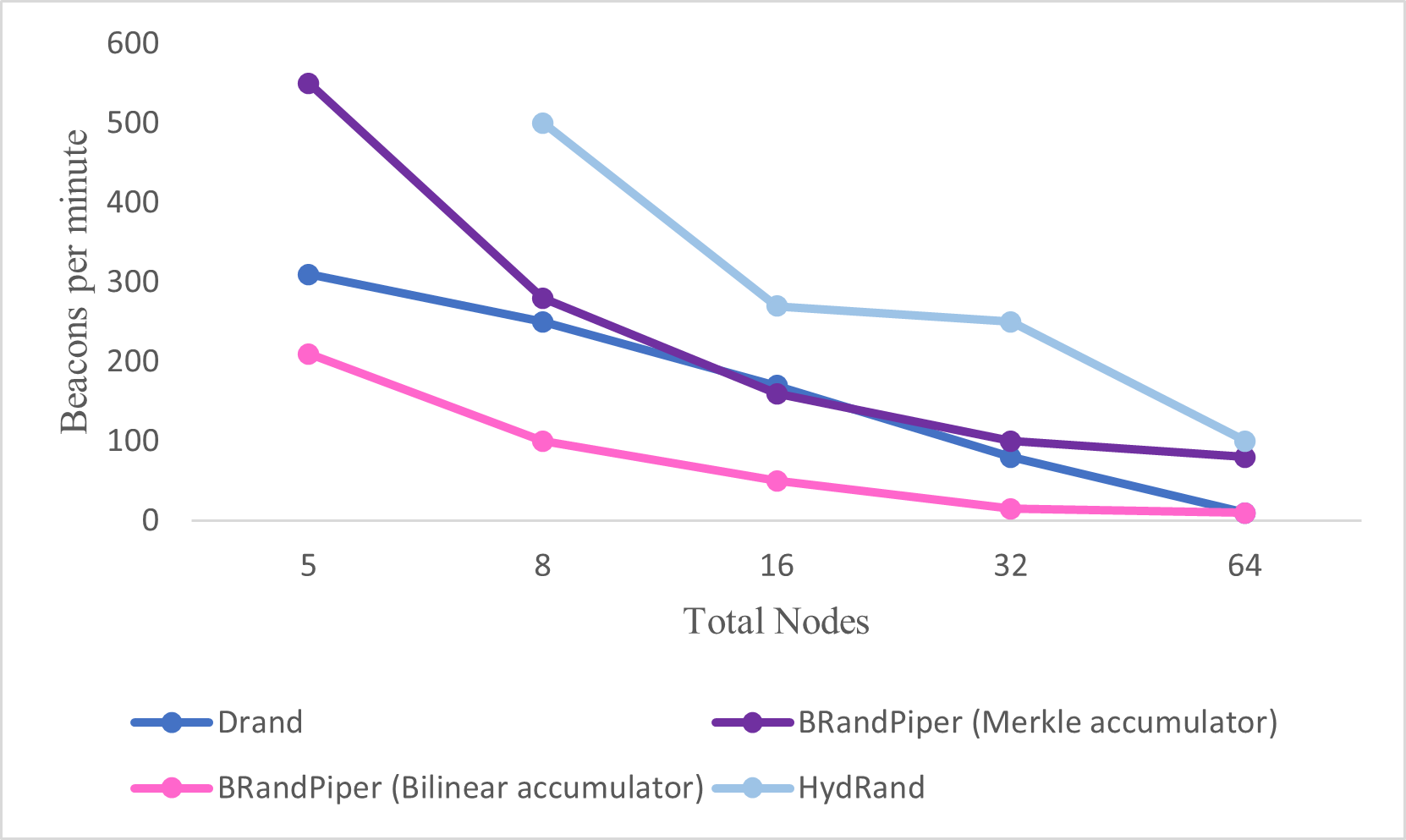
Figure 9 highlights a comparison between BRandPiper, HydRand and Drand (the beacon shown at the start of this blog) on beacons per minute. The contrast in practical efficiency is most apparent at smaller node numbers, with a more condensed distribution as 𝑛 increases and beacon generations approach an asymptotic floor. BRandPiper with a Merkle Tree accumulator is superior to Drand at lower and higher node numbers with negligible delta over the middle quantiles. HydRand is superior ∀𝑛 although this is at the expense of more restrictive fault assumptions and no absolute unpredictability.
Summary
Development of Random Beacon protocols has received increasing attention in recent years given their utility in a variety of use cases from auditing of government officials to proof-of-stake blockchain protocols and smart contracts. In this post we provided a definition for random beacon protocols, demonstrated a live implementation and explored three SOTA approaches.
Continue the discussion
Feel free to send me an email!
📧 will@willbosler.com



